Barcode-Scanner

Image by OpenClipart-Vectors from Pixabay

Barcodes sind im Alltag, insbesondere im Einzelhandel nicht wegzudenken. In diesem Projekt, das einer Idee von von Eckart Modrow folgt, soll versucht werden, das Grundprinzip von Barcodescannern nachzubilden.

Die folgende Animation zeigt eine mögliche Umsetzung:

Im Folgenden wird die Entwicklung des Barcodescanners skizziert. Eine vollständige mögliche Lösung ist auf Anfrage erhältlich.

Zunächst schauen wir uns den Aufbau eines bestimmten Strichcodes, dem EAN-8-Code, etwas genauer an:

Dieser besteht aus einer Folge von schwarzen (s) und weißen (w) Balken mit vier verschiedenen Breiten. An den beiden Rändern befinden sich jeweils drei Balken mit der kleinsten vorkommenden Breite in wechselnder Folge (sws). In der Mitte des Codes finden sich fünf ebenfalls schmale Balken in der Folge wswsw. Zwischen den Rändern und dem Mittelbereich sind jeweils 16 Balken (von links: 8 weiße und 8 schwarze) unterschiedlicher Breite. Jede Breite ist jedoch ein Vielfaches der minimalen Breite der Randbalken.

Jeweils vier Balken (oben rot umrandet) im Datenbereich kodieren eine Ziffer (insgesamt: 32 Balken ≙ 4 Zeichen). Wird der Code in aufrechter Lage von links nach rechts gescannt gilt folgende Codierung für eine Ziffer.

Breite der vier Balken swsw	codierte Ziffer
3211	0
2221	1
2122	2
1411	3
1132	4
1231	5
1114	6
1312	7
1213	8
3112	9

Dabei fällt auf, dass die vier Balken für eine Ziffer insgesamt immer eine Breite von 7 haben. Jeder Ziffer beansprucht also gleich viel Platz.

Für das Projekt sind lediglich zwei Sprites notwendig. Eines zur Darstellung des Barcodes mit einem passenden Kostüm und ein Sprite, das den Lichtpunkt des Scanners darstellt und die Skripte enthält.

Für den Scanner erzeugt man ein Kostüm, das aus einem möglichst kleinen Kreis besteht. Dies ist wichtig, weil wir später überprüfen wollen, ob dieses Sprite gerade schwarze oder weiße Bereiche berührt. Ist das Kostüm zu groß, können schmale Balken nicht sauber erfasst werden.

Zunächst bewegen wir den Scanpunkt von links nach rechts über das Zeichenfenster und speichern jeweils die x-Position in einer Liste , wenn ein Farbwechsel von weiß nach schwarz oder umgekehrt erfolgt.
Dazu nutzen wir zwei Hilfsblöcke und , die dafür sorgen, dass sich der Scanpunkt solange nach rechts bewegt, bis er wieder auf einen neuen schwarzen bzw. weißen Pixel trifft. Dies Blöcke sorgen also dafür, dass sich der Scanpunkt anschließend am linken Rand eines schwarzen bzw. weißen Balkens befindet.

Eine möglich Implementierung für :

Die Umsetzung für ist analog.

Mit einem geeigneten Skript speichert man nun die jeweiligen x-Koordinaten der linken Balkenränder in einer Liste:

Aus den Differenzen von je zwei benachbarten Positionen lassen sich die Breiten der Balken berechnen und in einer weiteren Liste abspeichern:

Die beiden letzten Balken können verworfen werden, da sie durch den rechen Bildschirmrand erzeugt werden.

Es fällt auf, dass sich die ermittelten Werte für gleich breite Balken unterscheiden können. Im Beispiel haben die schmalsten Balken eine Pixelbreite von 4,5 oder 6. Wir nutzen die ersten drei Balkenbreiten, um einen mittlere Balkenbreite für die schmalsten Balken zu berechnen:

Wir teilen wir nun alle Strichbreiten durch dies Einheitsbreite, runden auf ganze Zahlen und speichern dies Werte in einer neuen Liste . Das folgende Skript zeigt, wie man z. B. einen Datenbereich (16 einzelne Balken) zu den normierten Balkenbreiten 1-4 umrechnet.

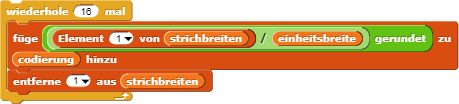
Die jeweils drei Balken der Randbereiche und die fünf Balken in der Mitte verwerfen wir dabei, so dass nur noch 32 Balken für die beiden Datenbereiche übrigbleiben:

Im letzten Schritt rechnen wir nun jeweils eine Folge von vier dieser Zahlen mit Hilfe obiger Tabelle zu einer Ziffer um. Die ermittelten Ziffern fügen wir nacheinander als Zeichen einer Variable an.

Um das Programm zu testen erzeugt man am besten mit einem EAN8-Generator aus dem Internet einige Codes, speichert sie als Bild und fügt sie als Kostüm für ein Sprite ein. Unter Umständen muss das Bild noch etwas vergrößert werden, damit die einzelnen Balken auch sauber erkannt werden können.

Das beschriebene Programm hat den Vorteil, dass die Barcodes nicht in einer bestimmten Größe vorliegen müssen. Außerdem wird der Code auch richtig erkannt, wenn der Barcode gegenüber der Bewegungsrichtung des Scanpunktes gedreht ist.